4.20 - Steekproefgrootte

4.20.1 Nauwkeurigheid en betrouwbaarheid

4.20.2 Berekening van steekproefgrootte

 

Stel dat de marktonderzoeker van alle elementen uit de populatie informatie betrekt. Hij kan dan zeer nauwkeurige en betrouwbare uitspraken doen over de populatie. Als de populatie (tamelijk) groot is, is dit erg duur, omslachtig en eigenlijk ook onnodig. Een representatieve steekproef geeft immers een goede afspiegeling van de populatie. Maar hoe groot moet een steekproef zijn om representatief te zijn? Dat hangt af van de gewenste nauwkeurigheid en betrouwbaarheid.

4.20.1 - Nauwkeurigheid en betrouwbaarheid

De marketeer moet op grond van steekproefonderzoek een marketingbeslissing kunnen nemen. Voor die beslissing is een bepaalde nauwkeurigheid in combinatie met een voldoende betrouwbaarheid van de uitspraak gewenst.

De vooraf gewenste nauwkeurigheid van een steekproefuitspraak is het maximaal aanvaardbare verschil tussen de uitkomst van de steekproef en de waarde van dezelfde variabele bij de hele populatie. Dit verschil wordt uitgedrukt in een marge rond de steekproefuitkomst. Dit maximaal aanvaardbare verschil heet nauwkeurigheidsmarge (nauwkeurigheidsinterval, betrouwbaarheidsinterval).

De vooraf gewenste betrouwbaarheid van een steekproefuitspraak is gelijk aan de kans dat herhaling van het steekproefonderzoek hetzelfde resultaat zou opleveren. Een betrouwbaarheid van bijvoorbeeld 95% betekent andersom dat in 100% - 95% = 5% van de gevallen een nieuwe steekproef van dezelfde populatie een uitkomst zou opleveren buiten het nauwkeurigheidsinterval.

CASUS
Marketeer Ellen Langleven wil onderzoeken hoeveel procent van de particuliere Hypercardhouders maximaal 1000 meter van een Hypervestiging woont. Van de uitkomst hangt af waar een nieuwe vestiging geopend kan worden. Dit zijn riskante beslissingen en daarom wenst marketeer Ellen Langleven een nauwkeurigheidsinterval van plus of min 1,5%van de steekproefuitkomst. Als de uitkomst van de steekproef bijvoorbeeld 20% is, wil zij erop kunnen vertrouwen dat met een betrouwbaarheid van bijvoorbeeld 95,6% tenminste 18,5% en ten hoogste 21,5% van de populatie maximaal 1000 meter van een Hypervestiging woont.

4.20.2 - Berekening van steekproefgrootte

Als een foute marketingbeslissing, die is gebaseerd op kwantitatief onderzoek, grote verliezen met zich zou meebrengen, eist men een hoge betrouwbaarheid en nauwkeurigheid van dat onderzoek. In de praktijk leidt dat tot een grotere steekproef. De statistiek levert mogelijkheden op om - gegeven een gewenste nauwkeurigheid en betrouwbaarheid - de steekproefomvang te bepalen.

TIP: Bepaal de gewenste nauwkeurigheid en betrouwbaarheid op basis van het risico dat je de verkeerde marketingbeslissing zou nemen als de steekproef toch niet genoeg representatief zou zijn.

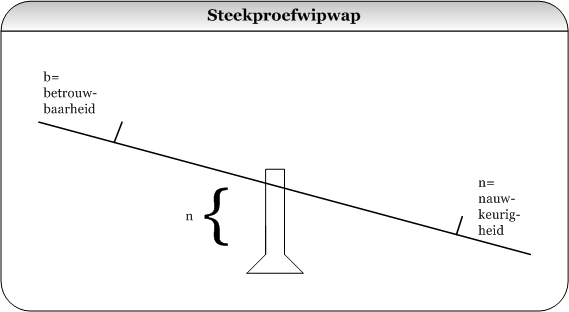
De onderstaande steekproefwipwap (figuur 4.8) introduceert de berekening van de steekproefgrootte.



Figuur 4.8 Steekproefwipwap

Op de steekproefwipwap zijn de hoogte van b (gewenste betrouwbaarheid) en nk (gewenste nauwkeurigheid) onderling van elkaar afhankelijk. Wil b kunnen stijgen (men wenst een betrouwbaarheid van 99,7% in plaats van 95%), dan zal nk automatisch dalen (waarbij de helft van het nauwkeurigheidsinterval groeit van 1,96 × standaardafwijking tot 3 × standaardafwijking). De enige manier om b en nk allebei te laten stijgen, of een van de twee te laten stijgen zonder dat de ander daalt, is: het scharnierpunt verhogen. Oftewel de steekproefgrootte te laten stijgen. Daarom staat n (steekproefgrootte) bij de stella¬ge van de wipwap.

We willen met een betrouwbaarheid van 95,6% een schatting maken van het percentage in de populatie, met een nauwkeurigheidsinterval van 3%. De berekening van de steekproefgrootte n gaat nu als volgt.

n = omvang van de steekproef (gevraagd), waarbij n = p x q / s2

p = uitkomst van de steekproef in procenten, waarbij p = 50 (per definitie, als uitkomt volledig onbekend is)

q = 100 – p = 50 (te berekenen)

s = standaardafwijking (te berekenen), waarbij s = nk : z (per definitie)

nk = gewenst nauwkeurigheidsinterval = 3% (gegeven)

z = halve breedte van het nauwkeurigheidsinterval, uitgedrukt in s (per definitie)

b = gewenste betrouwbaarheid = 95,6% (gegeven)

Als b = 95,6%, dan z = 2 (per definitie)

Dan s = nk : z = 3% / 2 = 1,5 (%)

We kunnen de formule voor de berekening van n nu als volgt invullen:

n = 50 x 50 / 1,52 ? n = 2500 / 2,25 ? n = 1111,111…

De steekproef moet (afgerond naar boven) 1112 elementen bevatten.